The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Šestiúhelník
Z Multimediaexpo.cz
m (Nahrazení textu) |
(++) |
||
| (Nejsou zobrazeny 3 mezilehlé verze.) | |||
| Řádka 3: | Řádka 3: | ||
Součet velikostí vnitřních [[Úhel|úhlů]] šestiúhelníku je přesně 720° (4π). | Součet velikostí vnitřních [[Úhel|úhlů]] šestiúhelníku je přesně 720° (4π). | ||
== Pravidelný šestiúhelník == | == Pravidelný šestiúhelník == | ||
| - | Vnitřní úhly pravidelného šestiúhelníku (všechny strany a úhly jsou si rovné) mají velikost 120°. Stejně jako [[čtverec|čtverce]] a [[rovnostranný trojúhelník|rovnostranné trojúhelníky]], lze i šestiúhelníky poskládat vedle sebe bez mezer a zcela tak vyplnit [[rovina|rovinu]]. Tímto způsobem jsou vytvářeny [[včela|včelí]] [[plástev|plástve]]. | + | Vnitřní úhly pravidelného šestiúhelníku (všechny strany a úhly jsou si rovné) mají velikost 120°. Stejně jako [[čtverec|čtverce]] a [[rovnostranný trojúhelník|rovnostranné trojúhelníky]], lze i šestiúhelníky poskládat vedle sebe bez mezer a zcela tak vyplnit [[rovina|rovinu]]. Tímto způsobem jsou vytvářeny [[včela|včelí]] [[plástev|plástve]]. |
=== Parametry === | === Parametry === | ||
Pro pravidelný šestiúhelník se stranou délky ''a'' platí: | Pro pravidelný šestiúhelník se stranou délky ''a'' platí: | ||
| - | * ''[[obvod]]:'' < | + | * ''[[obvod]]:'' <big>\(6\cdot a\)</big> |
| - | * ''minimální [[Průměr (geometrie)|průměr]]: < | + | * ''minimální [[Průměr (geometrie)|průměr]]: <big>\( a \sqrt{3} \approx 1,732 \cdot a\)</big> |
| - | * ''maximální průměr:'' < | + | * ''maximální průměr:'' <big>\(2\cdot a\)</big> |
| - | * ''[[obsah]]'':< | + | * ''[[obsah]]'':<big>\( \frac{3 \sqrt{3}}{2}a^2\)</big> |
=== Konstrukce pravidelného šestiúhelníku === | === Konstrukce pravidelného šestiúhelníku === | ||
Pravidelný šestiúhelník lze sestrojit s pravítkem a kružítkem. Následující animace vychází z [[Eukleidés|Eukleidových]] Základů, Kniha IV, Věta 15. | Pravidelný šestiúhelník lze sestrojit s pravítkem a kružítkem. Následující animace vychází z [[Eukleidés|Eukleidových]] Základů, Kniha IV, Věta 15. | ||
[[Soubor:HexagonConstructionAni.gif|center|Hexagon Construction Animation]] | [[Soubor:HexagonConstructionAni.gif|center|Hexagon Construction Animation]] | ||
| + | == Externí odkazy == | ||
{{Mnohoúhelníky}}{{Článek z Wikipedie}} | {{Mnohoúhelníky}}{{Článek z Wikipedie}} | ||
| + | [[Kategorie:Šestiúhelník| ]] | ||
[[Kategorie:Mnohoúhelníky]] | [[Kategorie:Mnohoúhelníky]] | ||
Aktuální verze z 15. 7. 2025, 12:18
Šestiúhelník je rovinný geometrický útvar, mnohoúhelník se šesti vrcholy a šesti stranami. Součet velikostí vnitřních úhlů šestiúhelníku je přesně 720° (4π).
Obsah |
Pravidelný šestiúhelník
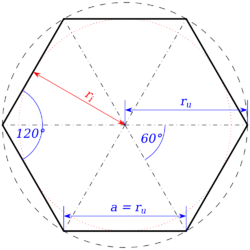
Vnitřní úhly pravidelného šestiúhelníku (všechny strany a úhly jsou si rovné) mají velikost 120°. Stejně jako čtverce a rovnostranné trojúhelníky, lze i šestiúhelníky poskládat vedle sebe bez mezer a zcela tak vyplnit rovinu. Tímto způsobem jsou vytvářeny včelí plástve.
Parametry
Pro pravidelný šestiúhelník se stranou délky a platí:
- obvod: \(6\cdot a\)
- minimální průměr: \( a \sqrt{3} \approx 1,732 \cdot a\)
- maximální průměr: \(2\cdot a\)
- obsah:\( \frac{3 \sqrt{3}}{2}a^2\)
Konstrukce pravidelného šestiúhelníku
Pravidelný šestiúhelník lze sestrojit s pravítkem a kružítkem. Následující animace vychází z Eukleidových Základů, Kniha IV, Věta 15.
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |